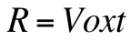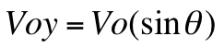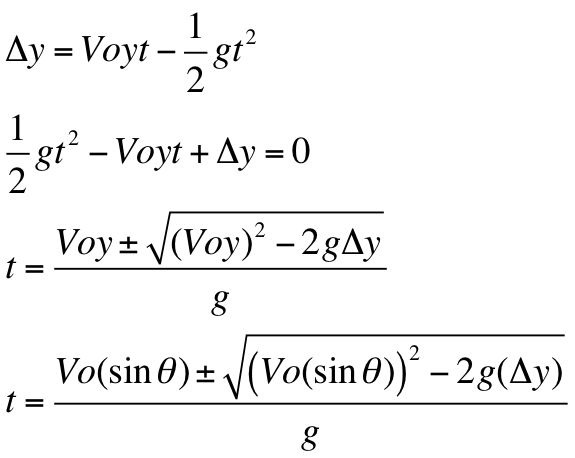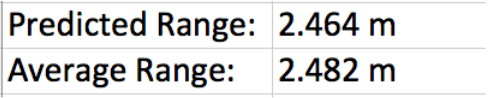Projectile Motion Lab
Author: Jacob Hoffner
Lab Partners: Andrea Schaefer and Connor Frey
Date: October 2015
Lab Partners: Andrea Schaefer and Connor Frey
Date: October 2015
Purpose
Projectile motion will be studied by resolving the initial velocity given to a ball. The range of a projectile will also be anticipated by using accumulated information, such as the initial velocity, angle of projection, change in height, and derived equations.
Theory
|
In order for us to anticipate an accurate projectile range, we utilize the projectile motion equations, along with the kinematic equations. Range can be found using: R = Vox(t). Since we do not know the initial horizontal velocity (Vox) or time (t), we must use different variables. According to what was discussed in class, we can derive an equation using other projectile motion equations.
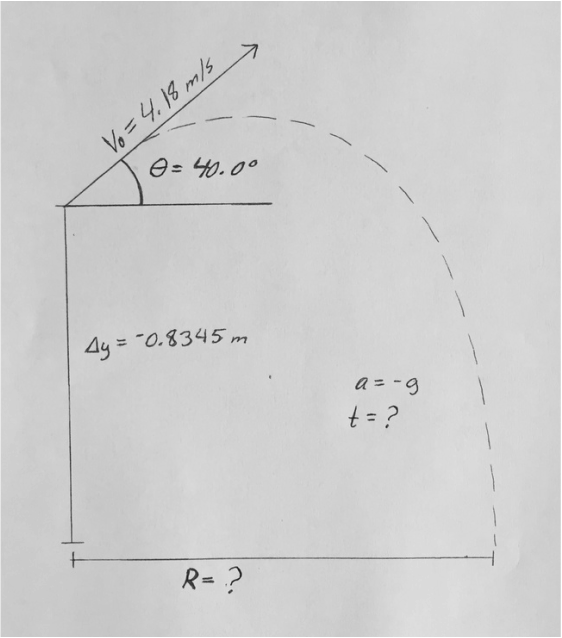
The diagram to the right illustrates the information known about the projected launch, along with the found range. |
Vox=?
Voy=? |
Experimental Technique
For this lab, we used a mini launcher to shoot a small ball a certain distance. First off, I set my angle of projection, measuring this accurately using a plumb bob. Using two photogates in front of the mini launcher, initial velocity was measured on a laptop through DataStudio. The change in height of the ball (delta y) was measured accurately using a plumb bob to mark the ground location on an index card and a tape measure to find the exact height of the ball before projection. Using the angle of projection, initial velocity and change in height that were found, we can predict the range of the projectile by deriving an equation. By shooting the projectile (ball) ten times, we can take an average of the ten shots onto a piece of carbon paper on top of our target paper to find an average range to see how accurate the predicted range was.
Data
The mini launcher projected the ball at an angle (θ) of: 40.0°
The initial velocity (Vo) of the ball as it left the mini launcher: 4.18 m/s
The change in height (Δy) of the projectile: -0.8345 m
The acceleration is gravity (-g), which is: -9.8 m/s squared
The initial velocity (Vo) of the ball as it left the mini launcher: 4.18 m/s
The change in height (Δy) of the projectile: -0.8345 m
The acceleration is gravity (-g), which is: -9.8 m/s squared
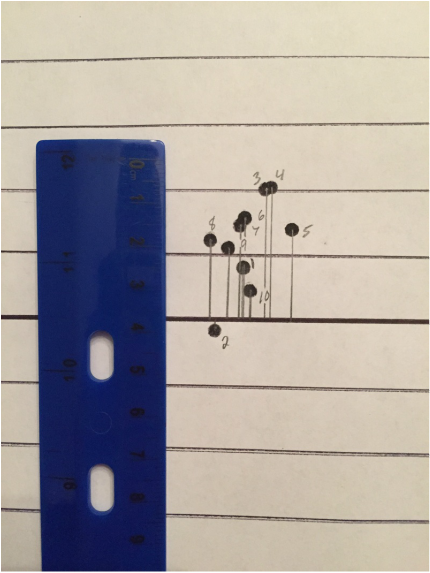
Below are the ten shots taken to find the average range. The dots on the right are numbered on the paper in order to correlate the distance and position of each dot with a value on the Shot/ Range chart to the left.
The Average Range is 0.018 meters greater than the Predicted Range.
The Percent Difference between the two is 7.279%.
The Percent Difference between the two is 7.279%.
Analysis
Below are the equations solving range and finding percent difference:
Range Equation:
Percent Difference Equation:
Conclusion
Throughout this lab, I have predicted the range of a projectile using a derived equation and certain variables, such as Vo, θ, and ΔY, in order to recognize how close my theory came to the average range found. By splitting the 0.033-meter difference between the highest range value and the lowest range value, I discovered that the range measurement uncertainty is 0.0165 meters. The predicted range was in close proximity with the average range; the 0.018-meter difference between the two ranges resulted in a percent difference of 7.279% . There were possible sources of error that were present in this lab. When aligning the mini launcher at 40.0° and the tape measure from the ground to the mini launcher using a plumb bob, parallax error could affect the resulting measurements due to the angle of observation. Moreover, human error in determining the last decimal place of the measured range values and the measured Δy value, as well as the placement of the range target paper at the predicted range measurement could affect the resulting average range. I do not think wind resistance is a factor in this lab. We performed this lab in an indoor environment that had no influence from outside factors. There was the possible chance of air movement due to the air conditioning/heating system and people moving about the room, however this air movement is so picayune that error caused to the lab from this factor would be too minuscule to show up in my data. The results of this lab concur with my theory, and demonstrate that one can virtually predict the range of a projectile by using the right procedures.
References
Giancoli, D. (1998). Chapter 3: Kinematics in Two Dimensions; Vectors. InPhysics: Principles with applications (5th ed., p. 1096). Upper Saddle River, N.J., New Jersey: Prentice Hall.
Bowman, D. (2015, October 1). Chapter 3: Kinematics in Two Dimensions; Vectors. Lecture presented at Physics, Lehighton.
Bowman, D. (n.d.). Lahs Physics. Retrieved October 1, 2015, from http://lahsphysics.weebly.com/
Bowman, D. (2015, October 1). Chapter 3: Kinematics in Two Dimensions; Vectors. Lecture presented at Physics, Lehighton.
Bowman, D. (n.d.). Lahs Physics. Retrieved October 1, 2015, from http://lahsphysics.weebly.com/