Ballistic Pendulum Lab
Author: Jacob Hoffner
Lab Partners: Zach Christoff and Alyssa Jordan
Date: January 2016
Lab Partners: Zach Christoff and Alyssa Jordan
Date: January 2016
Purpose
To investigate the conservation of momentum during a perfectly inelastic collision of a projectile through measure of an angle.
Theory
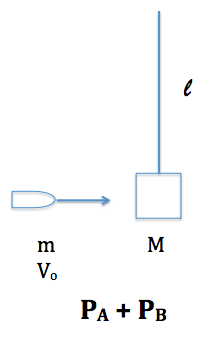
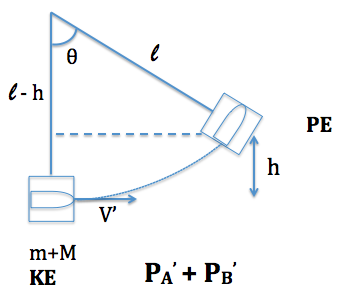
The Law of Conservation of Momentum states that the momentum of one object can affect the momentum of another object through a collision in a system. In this lab, we are to discover how the momentum of a projectile is to affect the final momentum in a pendulum. We are to investigate l (length), v0 (initial velocity), and mass m and M in order to find h (height), v' (final velocity), and theta (angle measure). By knowing the energies that pertain to the system and through the derivations of equations, we can find our unknown variables.
By setting the total momentums on each side of the collision equal to each other, we can derive an equation to solve for the final velocity. Since we know both masses (mass m and M) and the initial velocity of the projectile, we can find the final velocity.
Since we know the energies of the system and the now known final velocity, we can find height. We also know the acceleration of gravity.
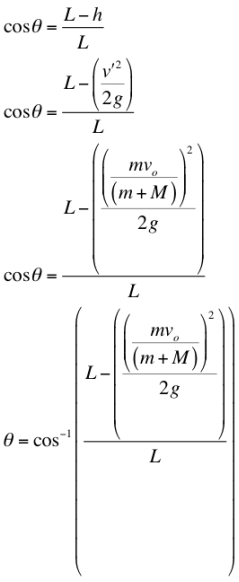
Now since every variable is found, we can find theta by deriving an equation, substituting the final velocity and height equations into an equation used to find theta.
Since we know the energies of the system and the now known final velocity, we can find height. We also know the acceleration of gravity.
Now since every variable is found, we can find theta by deriving an equation, substituting the final velocity and height equations into an equation used to find theta.
Experimental Technique
In order to conduct this lab, we first set up a projectile launcher to launch a projectile. This was attached to a pole, and on the top of the pole a pendulum was attached. The pendulum is connected to an angle measurer, which found the maximum angle the pendulum swung to. The velocity was measured using two photo gates attached to the front of the projectile launcher.
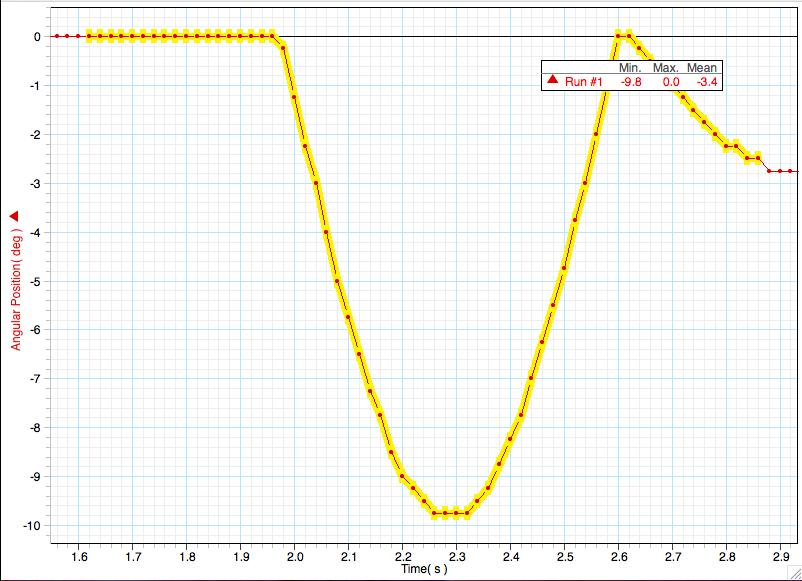
First, a projectile was launched in the projectile launcher three time, each time at a different setting of three settings. Each launch sent the projectile into the pendulum, which swung to a maximum angle measure. This angle measure was recorded in the connected computer using DataStudio.
Second, the pendulum was disconnected and the photo gates were attached to find the velocity of the three different settings for our projectile. The velocities were measured through the computer using DataStudio.
Thirdly, we measured the pendulum from the fulcrum at the top to the center of mass near the bottom in order to find l, or length. We also measured the pendulum for mass M and the projectile for mass m.
By plugging the velocities found and the masses found into the derived equation, we can find the final velocity, v'. Height, h, could also be found. Plugging all of this data into the derived theta equation enables us to find the calculated angle measures for all three launched projectile tests.
We can now compare the calculated angles found with the measured angles found earlier. By using percent difference, we can see how close they actually came to each other. Using this data, we can prove the Law of Conservation of Momentum.
First, a projectile was launched in the projectile launcher three time, each time at a different setting of three settings. Each launch sent the projectile into the pendulum, which swung to a maximum angle measure. This angle measure was recorded in the connected computer using DataStudio.
Second, the pendulum was disconnected and the photo gates were attached to find the velocity of the three different settings for our projectile. The velocities were measured through the computer using DataStudio.
Thirdly, we measured the pendulum from the fulcrum at the top to the center of mass near the bottom in order to find l, or length. We also measured the pendulum for mass M and the projectile for mass m.
By plugging the velocities found and the masses found into the derived equation, we can find the final velocity, v'. Height, h, could also be found. Plugging all of this data into the derived theta equation enables us to find the calculated angle measures for all three launched projectile tests.
We can now compare the calculated angles found with the measured angles found earlier. By using percent difference, we can see how close they actually came to each other. Using this data, we can prove the Law of Conservation of Momentum.
Data
Below are the measured and calculated angle measures found at the different launch settings. There are also the found initial velocities that the projectile had at launch.
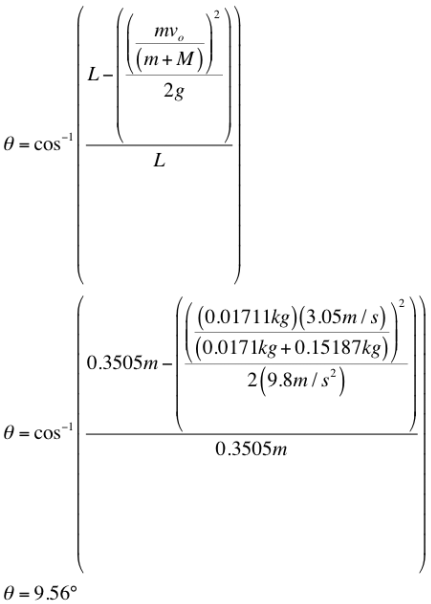
Mass of Pendulum Pole: 0.1711 kilograms
Mass of Projectile: 0.15187 kilograms
Length (l): 0.3505 m
Mass of Projectile: 0.15187 kilograms
Length (l): 0.3505 m
Analysis
Below are sample calculations of a calculated angle measure and percent difference.
Conclusion
In this lab, we were to investigate the momentum in a perfectly inelastic collision in a ballistics pendulum. By comparing the measured angles during the experiment with the calculated angles found, we discovered only a small percent difference in the comparison. The error in this lab could have been due to measurement/instrumental error in where we read each data point on DataStudio in order to claim what theta is. There could have been slight instrumental error in the device; it could have been slightly lose, causing a minuscule wobble during launching. Air resistance could have possibly played a very small role in slowing the pendulum. In order to solve the wobble problem, we can try to find a way to tighten the base of the projectile launcher/ pendulum. Overall, our theory was proven , as the derived equation led us to discover that the measured and calculated angle measures were very similar. The largest percent difference was only 3.8%. The derived equation proves (and overall theory proves) that momentum is conserved in a perfectly inelastic collision.
References
Giancoli, Douglas C. "Linear Momentum." Physics for Scientists & Engineers with Modern Physics. 4th ed. Upper Saddle River, NJ: Prentice Hall, 2000. Print.
Bowman, D. (n.d.). Lahs Physics. Retrieved October 1, 2015, from http://lahsphysics.weebly.com/
Bowman, D. (2015, October 1). Chapter 9: Linear Momentum. Lecture presented at Physics, Lehighton.
Bowman, D. (n.d.). Lahs Physics. Retrieved October 1, 2015, from http://lahsphysics.weebly.com/
Bowman, D. (2015, October 1). Chapter 9: Linear Momentum. Lecture presented at Physics, Lehighton.